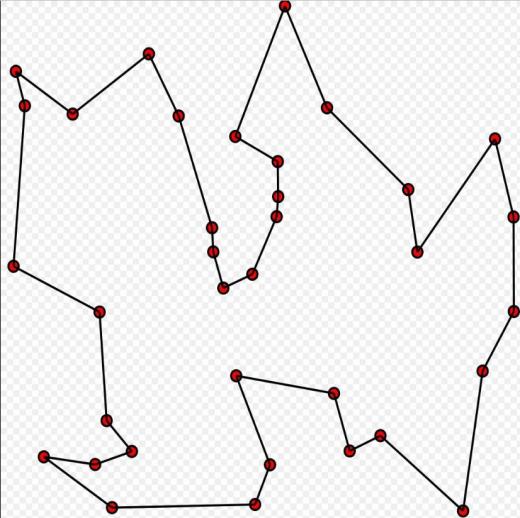
لكي تحل المعضلة التحسيبية التي في الصورة -معضلة البائع المتجول- فإنك تحتاج 8,400,000,000,000,000 سنة! يعني 8.4 كوادريليون سنة
هذي معضلة البائع المتجول، وباختصار فإن جملتها: عندك بائع يريد زيارة عدد معين من المدن، بحيث يمر على كل مدينة مرة واحدة فحسب من غير تكرار ويعود لنقطة البداية، بأقصر مسار ممكن.
الزمن المحسوب أعلاه هو في حالة أن البائع يبتغي زيارة 30 مدينة، ولأعطِ صورة عن التعقيد الحسابي للحالة، فلنستخدم مقاربة القوة العمياء Brute-force، والتي تعني استطلاع كافة المسارات الممكنة لإيجاد أقصرها؛ لِn من المدن، هنالك !(n-1) مسارات ممكنة، حيث ! يعبر عن المضروب Factorial، وذا يعني:
ل5 مدن لديك 24 مسارا محتمل
ل10 مدن لديك 362,880 مسارا محتملا
ل15 مدينة لديك 87,178,291,200 مسارا محتملا
ل20 مدينة لديك 60,822,550,204,416,000 مسارا محتملا
وكما ترى، فإن عدد المسارات المحتمل ينمو بشكل مرعب حرفيا عتد زيادة عدد المدن، والآن، لنفترض أن حاسوبا عملاقا يستطيع فحص 1 مليار (10⁹) مسارا في الثانية الواحدة، وبناءً على هذا الفرض فإنه يحتاج:
2 سنة ل20 مدينة
9,800,000 سنة ل25 مدينة
8,400,000,000,000,000 سنة ل30 مدينة
والآن، على فرض أن عمر الكون 13.8 * 10⁹ من السنوات، فإنك تحتاج 608,696 مرة من عمر الكون لكي تحل حالة ال30 مدينة!
يتبغ، مع عرض لخوارزمية هِلْد-كارب وخوارزميات التقريب والتحديس...
لكي تحل المعضلة التحسيبية التي في الصورة -معضلة البائع المتجول- فإنك تحتاج 8,400...